2011 ~ Mathematics Realm

December 28, 2011

SEASONS GREETINGS FROM REALM OF MATHEMATIC

2:00:00 PM Mathrealm No comments

MERRY CHRISTMAS

AND A

HAPPY NEW YEAR!!!

from REALM OF MATHEMATICS

THE MISSING COIN PROBLEM

1:22:00 PM Mathrealm 5 comments

Have you ever encountered the problem regarding the missing coin? Here it is:

A man wanted to buy a book worth 97 pesos but he does not have money for it. He decided to borrow from his friends. He borrowed 50 pesos each from his two friends. Now he has 100 pesos, which is enough to buy the book. He then bought the book and got a change of 3 pesos.

Since he still have 3 pesos, he decided to pay 1 peso each to his friends. He then only have 49 pesos credit from each of his friends.

The question is that, since he has 49 pesos credit for each friend and one peso at hand, that is
49 + 49 = 98 (credit from his friend
98 + 1 = 99 (the 1 peso is available at hand)

The total is 99 pesos but the original amount is 100 pesos. Where is the other one peso?

Post your answers here with your explanations...

________________________________________________________________________________

Note: All images used are with the permission of the owner, Mr. Ben Heine, a Belgian visual artist. You can visit his website and page at

http://www.benheine.com/
http://www.facebook.com/pages/Ben-Heine/45292293615

DIGITAL CIRCLISM

11:46:00 AM Mathrealm 3 comments

What are circles? How circles are used in works of art?

A circle is the set of all points equidistant from a fixed point called the center. Circles could be seen anywhere. The tires of a car, wall clocks, door knobs, plates, and other objects may come in circular shape. With all of these, I was truly amazed with the use of circles in artworks.

One of these are the works of Ben Heine. He used CIRCLES in forming photos/figures. He called them as DIGITAL CIRCLISM.

According to him, it is a modern artistic expression, a mix of Pop Art and Pointillism. It is made with digital tools usually featuring celebrities made of thousands of flat circles on a black background. Almost each circle has a different color, a different size and a different tone. One artwork generally took him about 100 to 180 hours.

Can you guess who are these?

1. E _ _ _ _ P _ _ _ _ _ _ ?

2. L _ _ _ G _ _ _?

3. M _ _ _ _ _ _ M _ _ _ _ _?

4. E _ _ _ _ _?

5. F _ _ _ _ _ _ M _ _ _ _ _ _?

6. J _ _ _ _ _ D _ _ _?

7. J _ _ _ _?

Circles are the main ingredients in the artworks above. See the beauty of circles? See the beauty of mathematics?

Now, it's time for you to guess who are in the images...

_________________________________________________________________

Note: All images used are with the permission of the owner, Mr. Ben Heine, a Belgian visual artist. You can visit his website and pages at
http://www.benheine.com/
http://www.facebook.com/pages/Ben-Heine/45292293615

THE SIGNIFICANCE OF 40 DAYS IN THE BIBLE

11:56:00 PM Mathrealm No comments

Photo Courtesy : Andrea Church/morgueFile

This is more than a month but God considers 40 DAYS a spiritually significant time period. Here are some situations in the Bible denoting the role of 40 DAYS:

> Noah's life was transformed by 40 DAYS of rain.

> Moses was transformed by 40 DAYS on Mount Sinai.

> The spies are transformed by 40 DAYS in the Promise Land.

> David was transformed by Goliath's 40-DAY challenge.

> Elijah was transformed when God gave him 40 DAYS of strength from a single

meal.

> The entire city of Ninevah was transformed when God gave the people

40 DAYS to change.

> Jesus was empowered by 40 DAYS in the wilderness.

> The disciples were transformed by 40 DAYS with Jesus after resurrection.

If God considered 40 DAYS as significant, then why don't we?

Now, ask yourself. "What can I do in 40 days that could change me and others for the better?"

Reference: Warren, R. (2004). The Purpose Driven Life. Quezon City: Purpose-Driven Ministries, Phil.,Inc.

MULTIPLYING NUMBERS BY 11

6:05:00 PM Mathrealm 1 comment

Photo Courtesy: Kirsty Hall/flickr

Photo Courtesy: Andrea Jaccarino/stock.xchng

If you were asked to multiply a given number by 11, how would you do it? I’m sure you’ll do the normal multiplication process like this:

x 11

253

Did you know that there is a simple way of multiplying a number by 11? You can multiply the numbers in a few second!

Let us use the previous example: (23)(11)

2 3 copy the digits of the number

2+3 = 5 add the digits

253 5 is written between 2 and 3

Therefore, (23)(11) = 253.

Let us have another example: (56)(11) = ?

5 6 copy the digits of the number

5+6 = 11 add the digits

(5+1) 1 6 since the result is a two digit number, retain the

ones digit and add the tens digit to 5

6 1 6

Therefore, (56)(11) = 616.

It is that easy! Now, it is your turn. Find the product of each pair of numbers.

1. (34)(11)

2. (45)(11)

3. (67)(11)

4. (85)(11)

5. (98)(11)

Answers:

1. 374

2. 495

3. 737

4. 935

5. 1,078

BASIC MATH QUIZ (Part I: Decimals and Integers)

4:34:00 PM Mathrealm 5 comments

Photo Courtesy: Aron/morgueFile

YEAR 2011

10:20:00 AM Mathrealm 1 comment

Photo Courtesy: grietgriet/morgueFile

Year 2011 is coming to an end. Before a new year comes, let us review things about 2011 that makes it somewhat special and amazing.

This year there are four (4) unusual dates. These are:
1) 01/01/11 or 1/1/11 = January 1, 2011
2) 01/11/11 or 1/11/11 = January 11, 2011
3) 11/01/11 or 11/1/11 = November 1, 2011
4) 11/11/11 = November 11, 2011

Another one is that October 2011 had 5 Sundays, 5 Mondays and 5 Saturdays.

Also, unusual result on the following:
Step 1: Get the last two digits of your year of birth.
For example, if you are born by year 1990, take 90.
Step 2: Add that number to your age this year..
In our example, if you were born year 1990, you will be 21.
90 + 21 = 111

The amazing thing about this is that no matter what year you were born, the result in step 2 will always be 111. Try it for yourself!

SQUARING NUMBERS ENDING IN 5

10:26:00 AM Mathrealm No comments

Photo Courtesy: Alvimann/morgueFile

What is 15²? How about 25²? How would you find the answer? Can you tell the answer in 3 to 5 seconds?

Yes, there is a fast way of squaring numbers ending in 5. The method lies on the pattern being formed by the numbers upon squaring as related to the numbers being squared. Let's observe the pattern of the numbers.

    5² = 25

    15² = 225

    25² = 625

    35² = 1,225

We know already that 5² is equal to 25, that is 5² = (5)(5) = 25. Since the remaining numbers end in 5, expectedly the results should also end in 25.

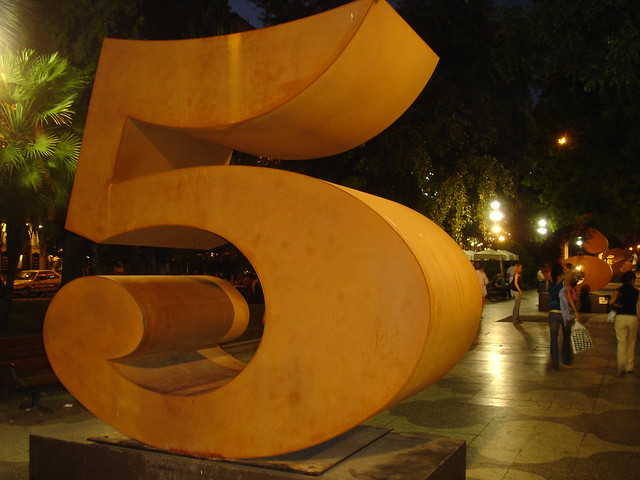Photo Courtesy: losmininos/flickr

15 ² = 225
25 ² = 625
35 ² = 1225

Now, let us look for the relationship between the remaining digits (aside from 5 and 25). The numbers are

   1 and 2    where     2 = (1)(2)
   2 and 6 6 = (2)(3)
   3 and 12 12 = (3)(4)

In the first pair of numbers, 2 is the product of 1 and the next consecutive number which is 2. Same as with the second pair, 6 is the result when 2 is multiplied to the number next to it which is 3. In the third pair, 12 is the product of 3 and 4.

Hence, when you square a number ending in 5, you simply multiply the remaining digit of the number, aside from 5, to the number next to it. Let us try to use it in the following numbers.

What is 45²?

solution:

Since the other digit aside from 5 is 4, multiply it to the number next to it which is 5. That is

(4)(5)= 20

Affix 25 to the result. The result is 2025.

Hence, 45²=. 2,025

Find the exact value of 55²?

solution:

The number is 5. Multiply that to the next number 6.

(5)(6) = 30

Affix 25 to it. That is 3,025.

Hence, 55² = 3025.

Now, it's your turn. Try to find the value of the following in 5 seconds.

65²

75²

85²

95²

105²

THE 3 CATS, 3 MICE PROBLEM

7:26:00 PM Mathrealm 6 comments

Photoi Courtesy: chaka/morgueFile

It takes five (5) cats to catch five (5) mice in five (5) days. How long would it take for three (3) cats to catch three (3) mice?

Please post your answer with corresponding explanation / solution here.